Меридианная проекция - вода: различия между версиями
(→второй пример) |
|||
| Строка 1: | Строка 1: | ||
[[Category:Меридианная проекция]] | [[Category:Меридианная проекция]] | ||
[[Category:Модель рельефа Земли]] | [[Category:Модель рельефа Земли]] | ||
| − | + | {{live|17024}} | |
| + | Удобно изучать Землю в разрезе меридианов. | ||
= Самая простая модель = | = Самая простая модель = | ||
Создадим самую простую модель Мирового океана. | Создадим самую простую модель Мирового океана. | ||
| − | Игнорируем сушу и дно. | + | Игнорируем сушу и дно. Интересует только водой. |
= Как считать уровень воды = | = Как считать уровень воды = | ||
| Строка 21: | Строка 22: | ||
Рассчет происходит по такому алгоритму: | Рассчет происходит по такому алгоритму: | ||
# начальные условия: {{fine|спокойная Земля#сферические координаты|sym=,}} | # начальные условия: {{fine|спокойная Земля#сферические координаты|sym=,}} | ||
| − | |||
| − | |||
| − | |||
| − | |||
# | # | ||
#* на входе: {{sym|тазик#высота|fine=,|строка=скобки}} и {{sym|градиент#волнения|строка=скобки}} | #* на входе: {{sym|тазик#высота|fine=,|строка=скобки}} и {{sym|градиент#волнения|строка=скобки}} | ||
Версия 13:22, 13 февраля 2019
комментарии в LiveJournal Удобно изучать Землю в разрезе меридианов.
Содержание
Самая простая модель[править]
Создадим самую простую модель Мирового океана.
Игнорируем сушу и дно. Интересует только водой.
Как считать уровень воды[править]
Имеем один меридиан, разделенный на тазики от северного полюса до южного.
Для расчета уровней воды в тазиках выбираю сферические координаты.
Другие виды координат не подходят, потому что:
- в геоцентрических координатах радиус не перпендикулярен датуму, и градиент спокойствия равен нулю. Но при изменении уровня воды градиент спокойствия становится не равным нулю, поэтому расчеты нужно отвязывать от датума, а по определению это нельзя делать.
- в геодезических координатах радиус перпендикулярен датуму, и градиент спокойствия равен нулю, но для несбалансированной воды радиус настолько изменчив, что объемы соседних тазиков пересекаются, а это усложняет расчеты.
В сферических координатах радиус не перпендикулярен датуму, и градиент спокойствия не равен нулю. Эта особенность позволяет отвязываться от датума и переходить от одного к другому. Также для несбалансированной воды, и при изменении уровня воды радиус стабилен.
Алгоритм[править]
Рассчет происходит по такому алгоритму:
- начальные условия: спокойная Земля, сферические координаты
-
- на входе: [math]h_{OQ}[/math] (тазик, высота) и [math]\nabla{g}_e[/math] (градиент волнения)
- изменение градиента сохраняет объем воды тазика с высокой точностью благодаря симметричности в сферических координатах
- на выходе: [math]V_{to}[/math] (тазик, объёмы перетекания), которые нужно перелить через каждое из 4 общих ребер
- перелить воду
- на выходе: [math]h_{OQ}[/math]
- идти на п.2
пересчитывать [math]\nabla{g}_q[/math] (градиент спокойствия) при изменении [math]a[/math] - Эллипсоид, большая полуось, [math]g[/math] - [[|]], а также при значительном изменении [math]h_{OQ}[/math]
Примеры[править]
На следующих изображениях северных полюс находится вверху, южный - внизу. Экватор посередине.
Слева направо возрастает модельное время, то есть левая сторона изображения показывает начальные условия.
Глубины отсчитываются относительно формы Земли в эллипсоидальном приближении. Нулевая отметка глубины окрашена в зелёно-синий цвет (Aquamarine).
Закругленности вверху и внизу оставлены для красоты...
первый пример[править]
Один тазик поднимается с глубины 500м, а другой опускается с высоты 500м:
Видно, что вода падает и поднимается, сохраняя неестественную отвесность сторон тазиков. Это вызвано тем, что вода перетекает через ребра верхней грани, а не через ребра сторон.
Возникающая волна выглядит естественно.
второй пример[править]
Уменьшаем центробежное ускорение, увеличивая звездные сутки сначало немножно (от 23,9 часов до 26,7), а в середине времени резко до 46,2 часов
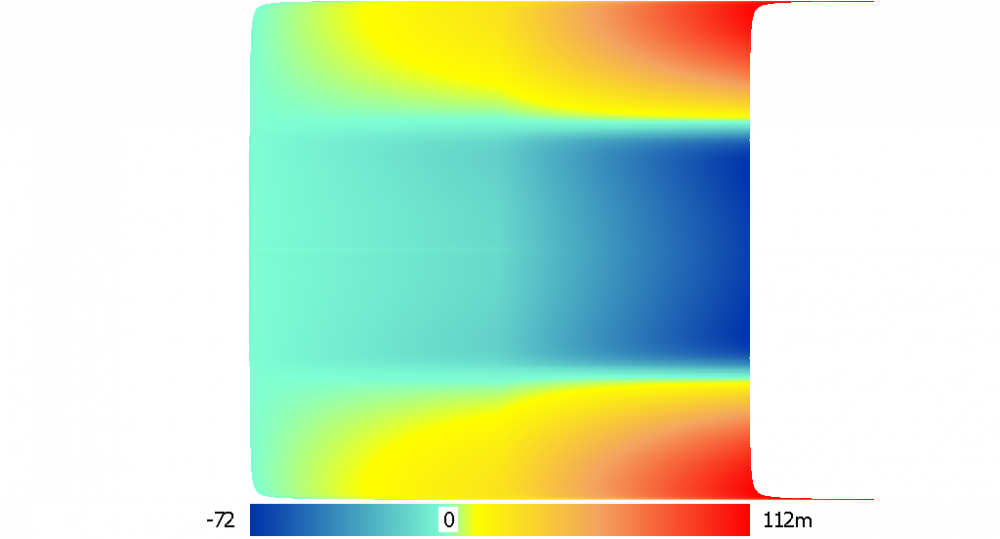
Видно, что высота волн постепенно увеличивается и смещается к полюсам.
Можно посмотреть в изменяющемся масштабе, когда на каждый момент времени масштаб выбирается таким, чтобы экстремальные значения были выделены самым контрастным цветом
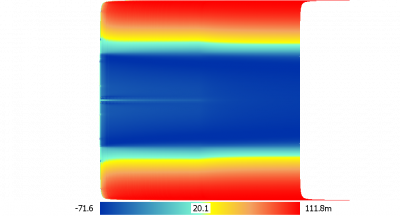
Легенда показывает масштаб для последнего момента, когда рост волны рост волны не останавливается.
Высота волны в 172 метра (разница между полюсами и экватором) - это конечно, мало для данного случая, но здесь я столкнулся с ограничениями компьютера.
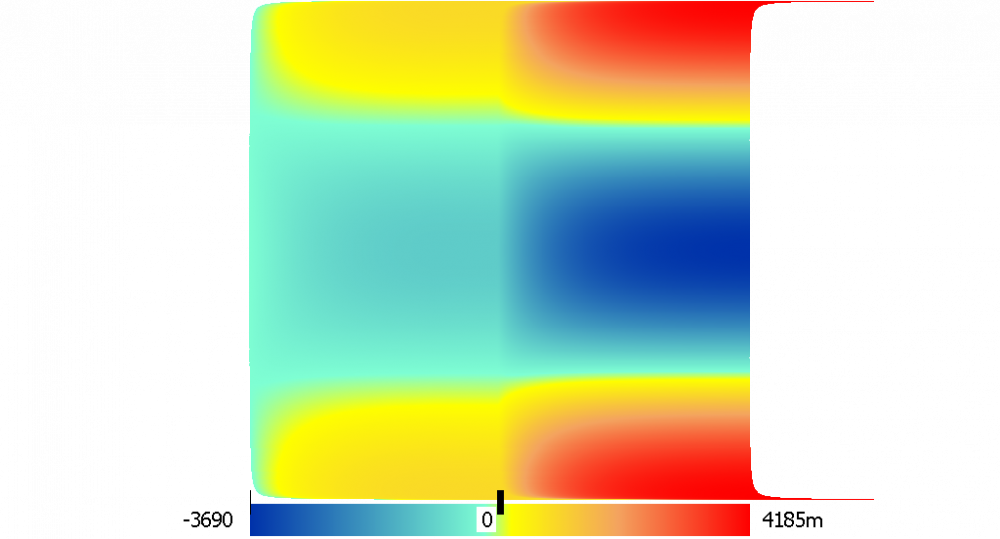
Увеличив время интегрирования от 5 до 1000, была получена высота волны в 7 километров, но компьютер шел к этому около получаса, что есть неудобно.
Выводы[править]
Нужно сопоставить время интегрирования с точностью результата, и в дальнейшем добавить с модель сушу и рельеф дна.