Переход на матричные преобразования
Перейти к навигации
Перейти к поиску
комментарии в LiveJournal
и снятся парты аудиторий[править]
Ещё недавно косинусы углов считал функцией System.Math.Cos().
Углов стало больше - перешел на скалярное произведение единичных векторов. Крайние условия для тех, что коллинеарны, пришлось тщательно описывать, куда же денешься.
И тут понял, что матричные преобразования компактнее, учитывают крайние условия, считают косинусы связанных углов и проще оптимизируются.
Вот результирующий код для расчета матрицами:
var aOnSurface = axisOrtohonal.Direction * b.Matrix;
aTraverse = -a * aOnSurface[1];
var aMerid = (b.Vartheta < 0 ? 1 : -1) * a * aOnSurface[2];
return aMerid;
и вот для сравнения, как считалось скалярным произведением вначале:
var surfaceCalm = new Plane(b.NormalCalm, b.r);
var QonAxisPlane = new Plane(axisEnd, b.Q3, Basin.O3);
// aSphere direction
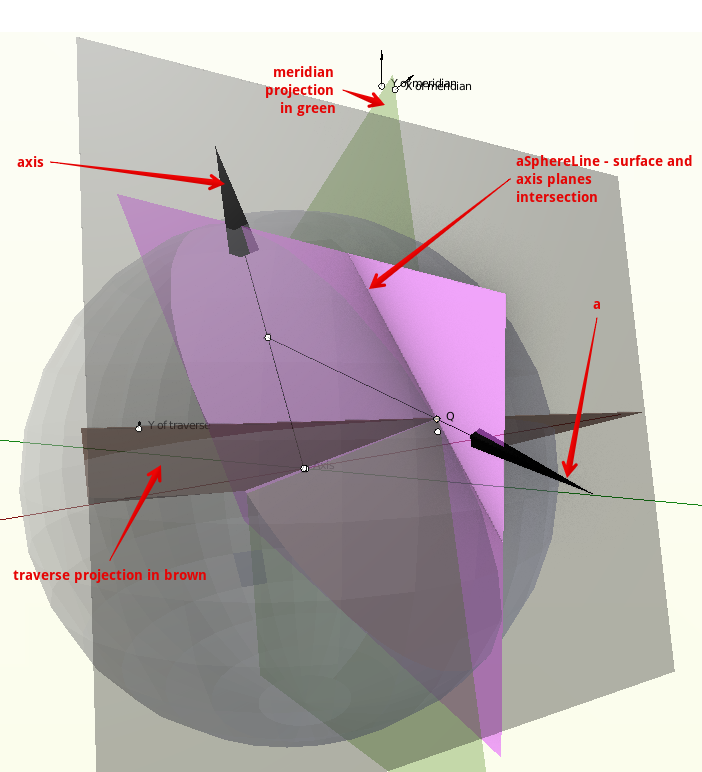
var aSphereLine = surfaceCalm.IntersectionWith(QonAxisPlane);
var b3unit = new Line3D(Basin.O3, b.Q3).Direction;
// lays in surfaceCalm plane, directed to equator of AxisOfRotation if Math.Abs used
var aSphere = //Math.Abs
(a * AxisOfRotation.DotProduct(b3unit));// axisOrtohonal.Direction.DotProduct(aSphereLine.Direction));
var aMeridianLine = surfaceCalm.IntersectionWith(b.MeridianCalm); //new Plane(OzEnd, Q3, O3);
var aTraverseLine = surfaceCalm.IntersectionWith(b.TraverseCalm);
Assert.AreEqual(0, aMeridianLine.Direction.DotProduct(aTraverseLine.Direction), .000000001);
aTraverse = Math.Abs(aSphere * aSphereLine.Direction.DotProduct(aTraverseLine.Direction));
var planeOZ = new Plane(Basin.Oz);
var planeAxis = new Plane(AxisOfRotation);
//directed to equator of Oz if Math.Abs used
double aMeridian;
/*if (aSphereLine.IsCollinear(aMeridianLine, .1))
{
aMeridian = aSphere;
}
else*/
{
var dotProduct = aSphereLine.Direction.DotProduct(aMeridianLine.Direction);
aMeridian = Math.Abs(aSphere * dotProduct);
}
// if (AxisOfRotation != Basin.Oz)
var spin = new Plane(Basin.OzEnd, b3unit.ToPoint3D(), axisEnd).Normal.DotProduct(b3unit);
// "north" hemisphere of AxisOfRotation
if (b3unit.DotProduct(AxisOfRotation) > 0)
{
if (spin > 0)
{
aTraverse = -aTraverse;
}
}
else
{
if (spin < 0)
{
aTraverse = -aTraverse;
}
}
//aMeridian<0 if Q3 between planes or inside of cones (bug when angle is near 90) of OZ and AxisOfRotation
if (planeOZ.SignedDistanceTo(b.Q3) * planeAxis.SignedDistanceTo(b.Q3) < 0)
{
aMeridian = -aMeridian;
}
else
{
var coneAxis = new UnitVector3D((Basin.Oz + AxisOfRotation).ToVector());
if (new UnitVector3D(b.Q3.ToVector()).DotProduct(coneAxis) > coneAxis.DotProduct(Basin.Oz))
{
//inside cone
aMeridian = -aMeridian;
}
}
return aMeridian;